As we have previously stated, our project involving AA 7075-T6 consists of two states, the matrix and the micron-sized particles. It is known that the majority of these particles are either iron-aluminum based or magnesium-silicide based [1]. In general, it has been found that these course particles are between two and three times harder than the surrounding matrix [1]. In our opinion, it could be extremely beneficial to investigate the contrast of the microstructure in the case of the matrix and the particles.
Our plan moving forward is to make use of the program, Materials Knowledge Systems (MKS), developed by Dr. Kalidindi. In his work, he has shown that MKS for first-order influence coefficients can make accurate predictions for contrast ratios of up to 1.5 [2]. However for higher contrasts, it is necessary to make use of higher order influence coefficients to make accurate predictions. Detailed in the same paper, the MKS model with second-order coefficients are tested against microstructures with contrast ratios of 5 and 10. It was found, under a contrast of 5, that using an MKS approach with second-order coefficients up to the first neighbors, MKS yielded a 4.88% error in the prediction of strain distributions [2]. 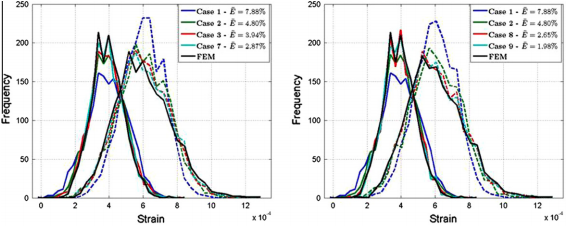 [2]
[2]
In terms of minimizing costs from calculations, the second-order first neighbors method is chosen for our example as the predicted distribution has previously been shown to be significant at a 95% level for a contrast of 5. Since we need only to deal with contrasts of at most 3, this method should be the best to use. Furthermore it should not be necessary to compute predictions using more than the first neighbors as it was also shown in [2] that additional neighbor calculations yield only modest improvements.  [2]
[2]
[1] Rollett Et al, 2006, “Three Dimensional Microstructures: Statistical Analysis of Second Phase Particles in AA7075-T651”, Materials Science Forum, Vols. 519-521, pp 1-10 [2] Fast T, Kalidindi SR. “Formulation and calibration of higher-order elastic localization relationships using the MKS approach.” Acta Materialia, 59 (2011), 4595-4605