Simulation parameters
The following data is computed using the first order MKS influence coefficients to predict a full strain tensor. These coefficients were trained on a 21x21x21 volume. The simulated volume is a 100x100x100 volume constructed using David Turners neighborhood optimization code with 1.8% volume fraction of particles. The final damage prediction uses the methodology introduced in the previous post. The results are binned by the Euclidean distance to the nearest particle to understand damage variation as we approach a far-field value. All plots use the same 50 bins for direct comparison of the relative frequency values as well as having a sufficient ( > 10) number of values in each bin.
Comparison of two literature loading conditions
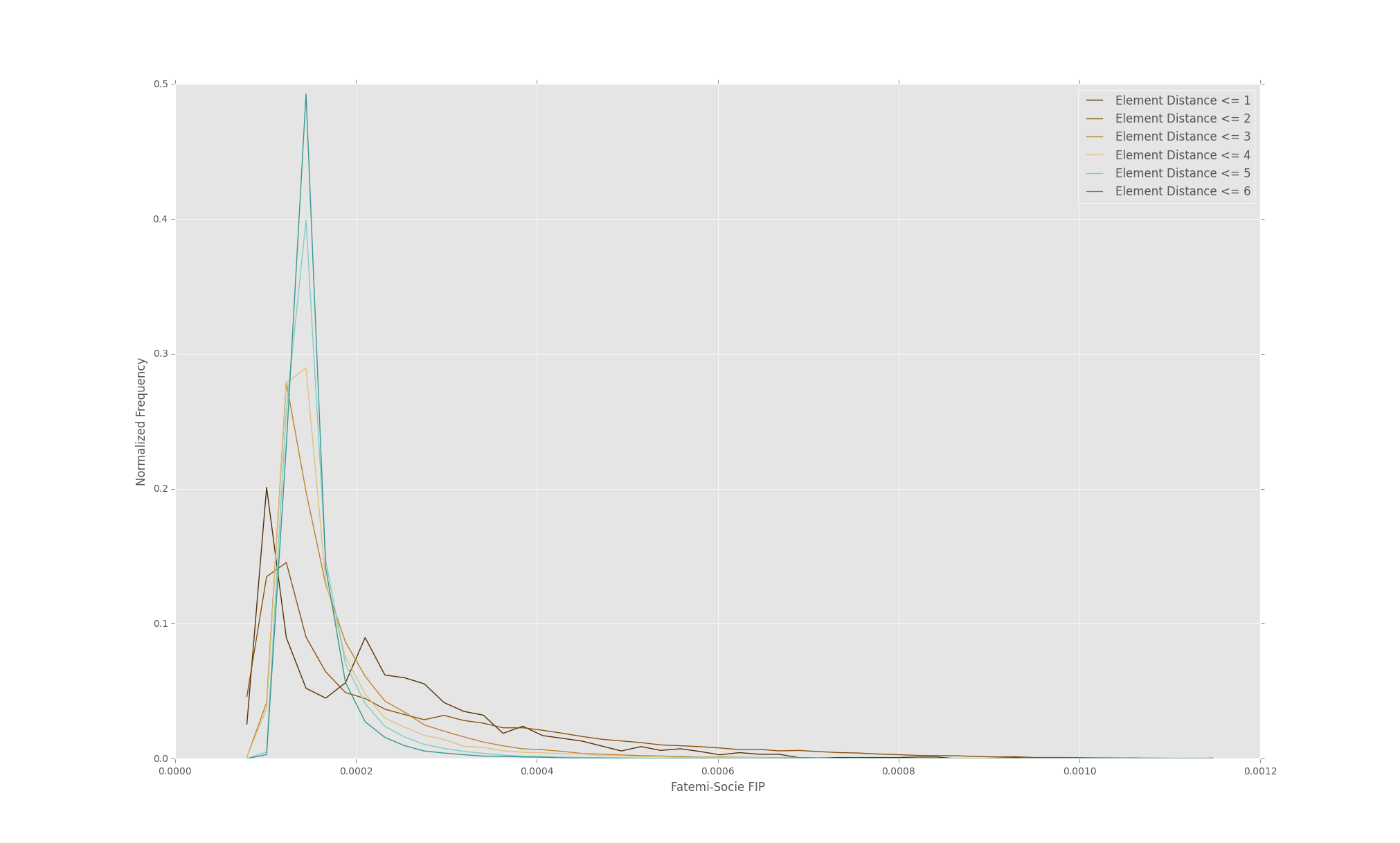 Shear loading at 0.004 amplitude
Shear loading at 0.004 amplitude
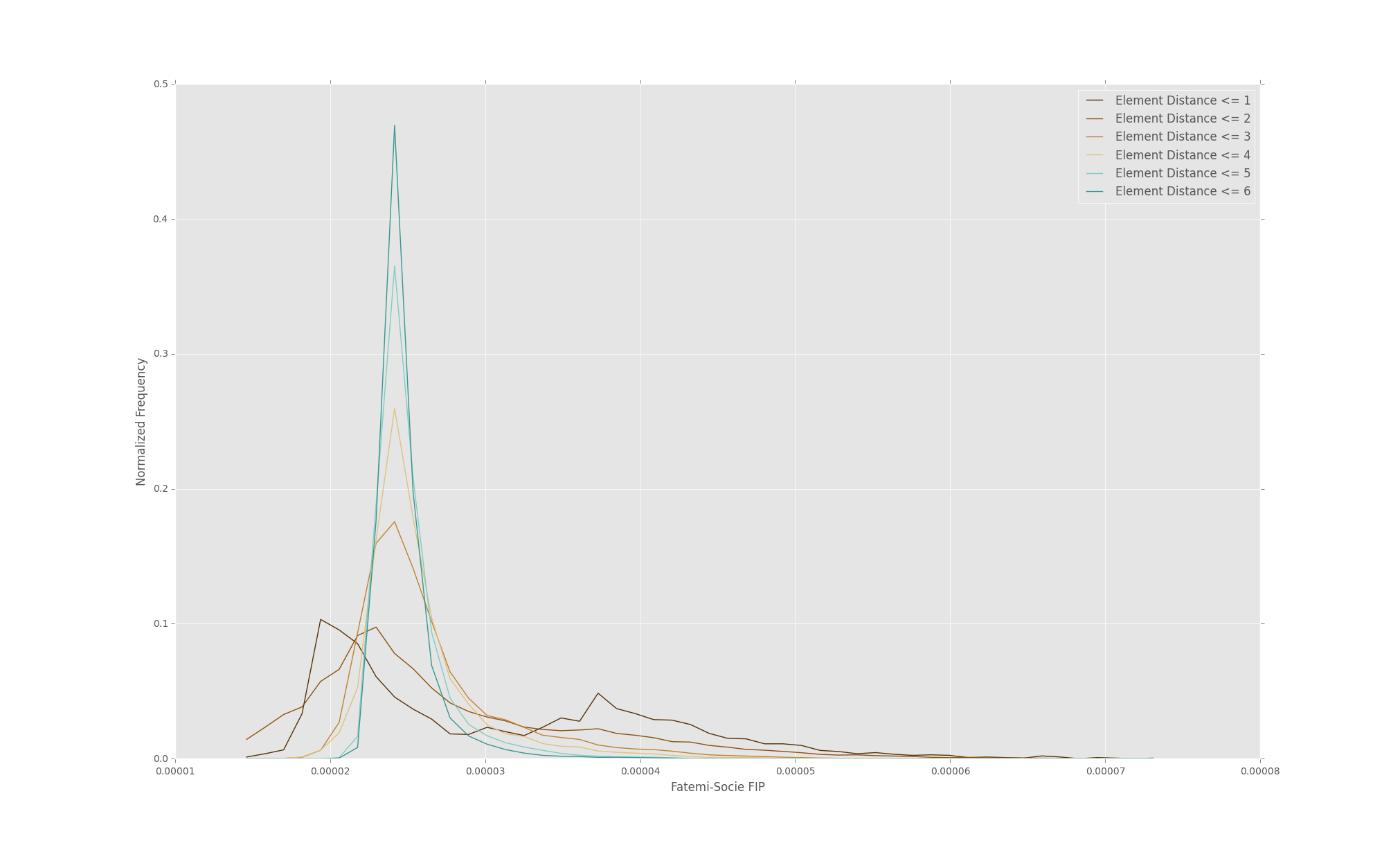 Uniaxial loading at 0.002 amplitude
Uniaxial loading at 0.002 amplitude
Several interesting features become readily apparent in the plots here. The first is that both loading conditions do indeed quickly approach a far-field condition. For this reason, both plots are restricted to the first 6 spatial bins. Another feature is that both loading conditions appear to produce a bimodal distribution. The uniaxial distribution has the second peak at a higher FIP value which should degrade the fatigue lives as indicated by the literature. This is likely due to the anisotropic particle distributions oriented in the loading distribution, and indeed what we initially wanted to confirm via MKS.
Future efforts
Our final work will be to confirm the cause of the increased damage in the uniaxial loading condition as well as performing multiple predictions to understand some of the variability in fatigue lives as well. If these efforts are successful, the MKS predictions will be incorporated into a multi-stage fatigue life prediction using explicit cracking and long crack predictions.