Tools and criteria
The main tool we used for the model generation is R. We use the step-wise regression tool in R that uses the AIC (Akaike Information Criteria). To apply AIC in practice, we start with a set of candidate models, and then find the models’ corresponding AIC values. There will almost always be information lost due to using a candidate model to represent the “true” model (i.e. the process that generates the data). We wish to select, from among the candidate models, the model that minimizes the information loss. We cannot choose with certainty, but we can minimize the estimated information loss. The preferred model is the one with the lowest AIC
We will also take into account the R-squared value of the model as well as the p-value of the variables (The smaller the p-value, the larger the significance of the variable.)
Regression results using the variables as the estimators
Example of the dartdrop property
The dartdrop test measures the puncture resistance of the polymer film. We 4 linear regression model using our variables as an estimator. The variables of interest were automatically chosen using the step-wise regression.
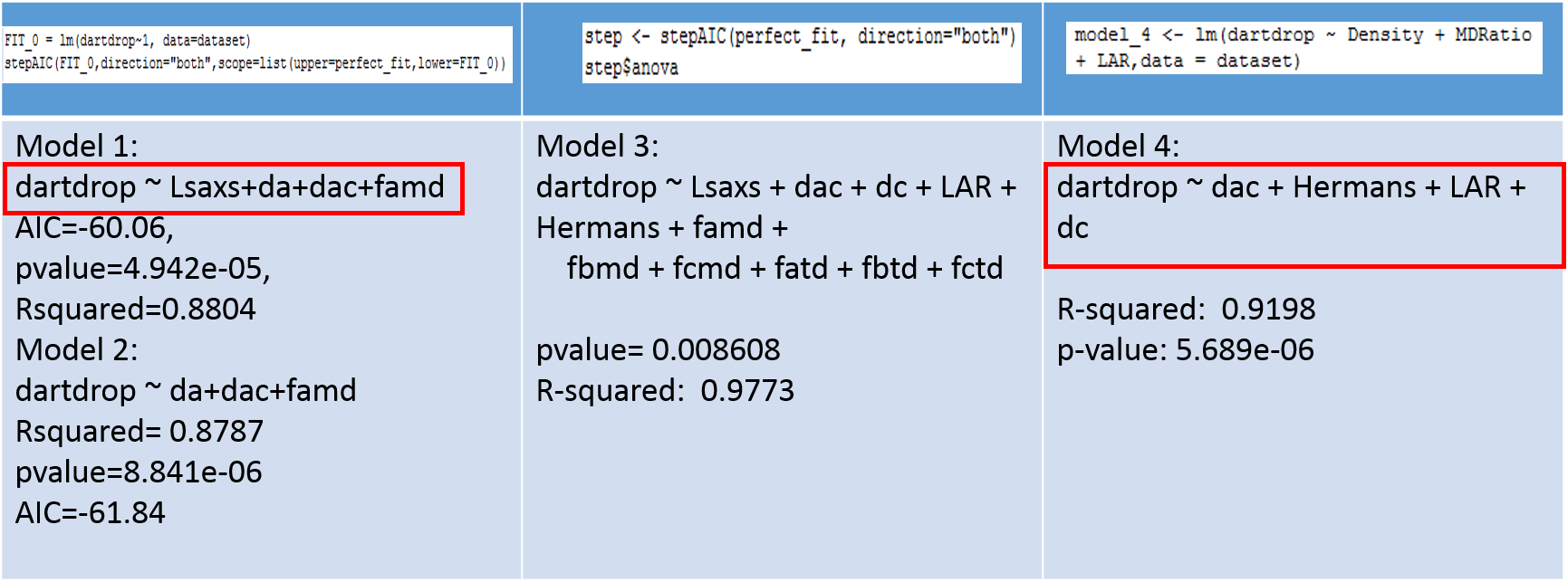
We need to compromise between a good R-squared and the least number of variables. So we will keep the 2 models in red. We can also notice that we don’t necessarily have the same variables in the 2 models chosen. The fact that all these variables have close relative importance is showing up here.
Cross-validation
Let’s know look at the cross validation results of these 2 models. We used a 2-fold cross validation. The initial sample is randomly partitioned in 2 sets: fold 1 and 2. We then train on fold 1 and test on fold 2, followed by training on fold 2 and testing on fold 1.
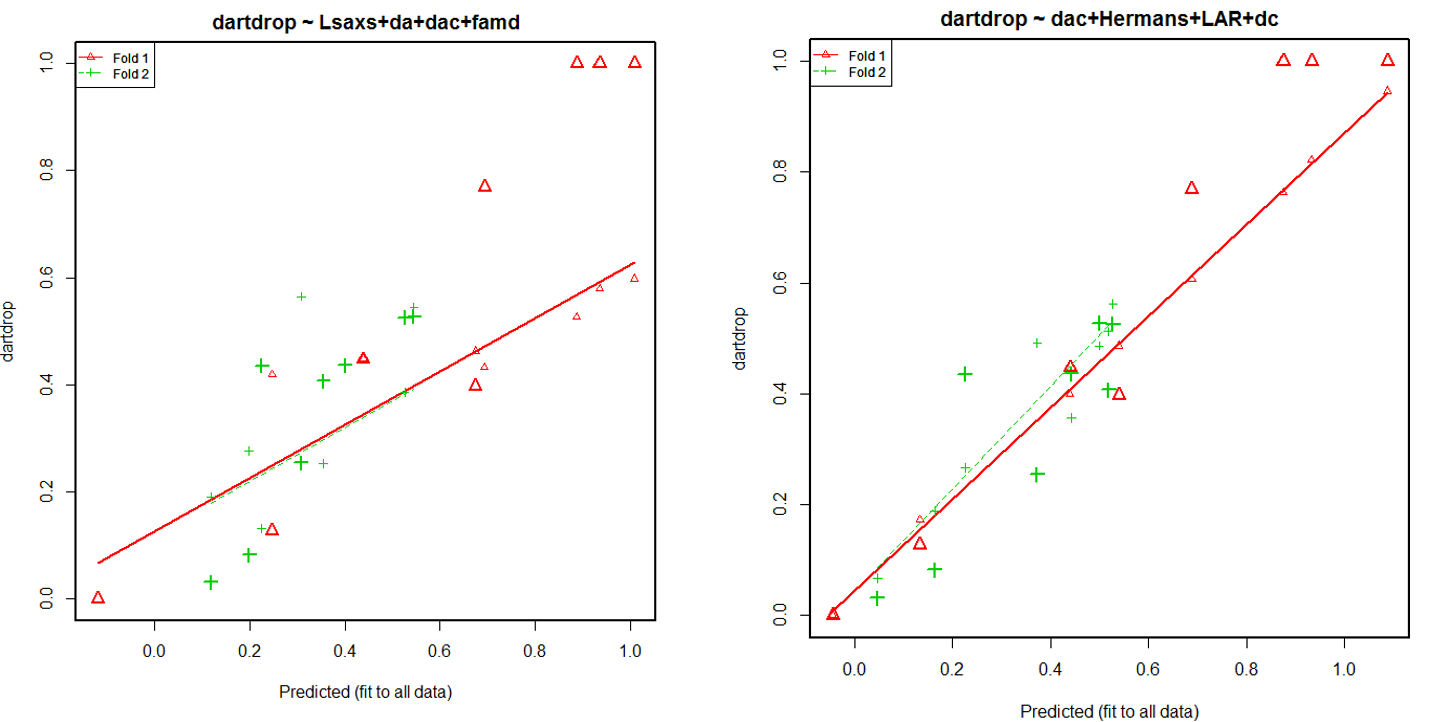
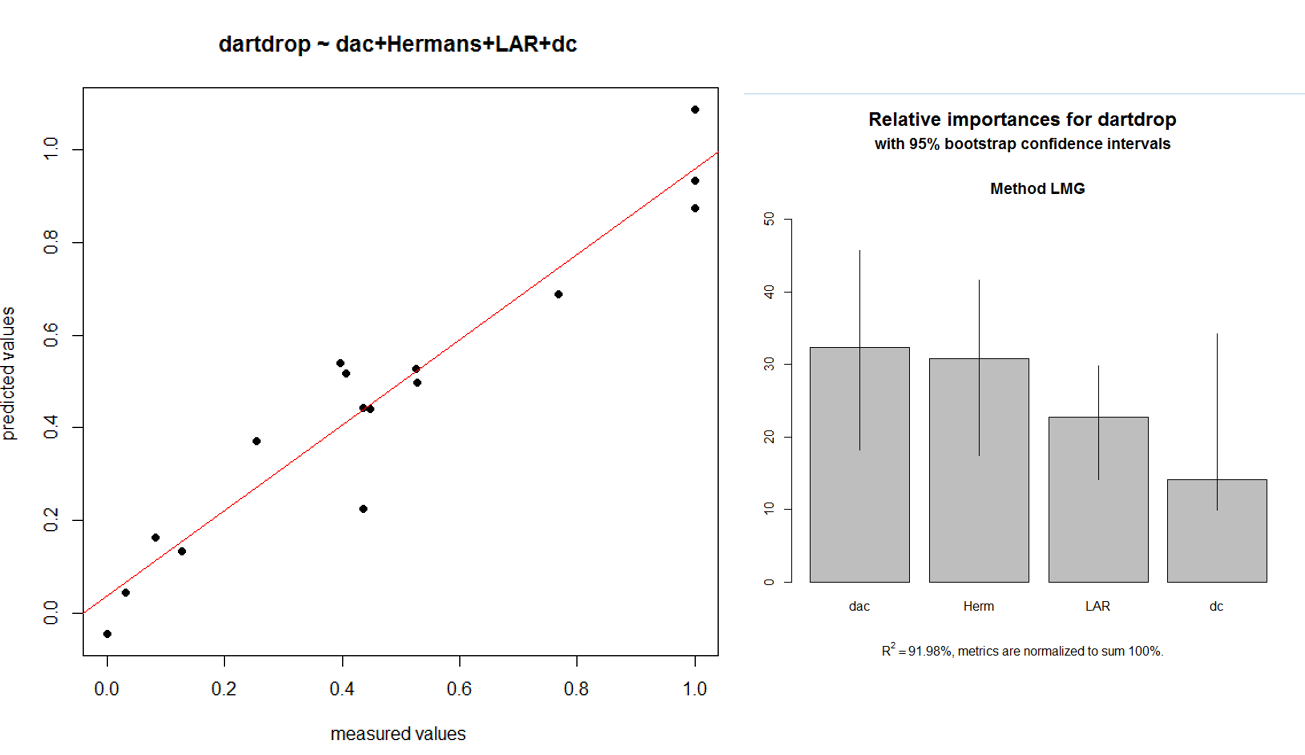
The first model (dartdrop ~ Lsaxs+da+dac+famd ) shows better results at the cross validation than the second one (dartdrop ~ dac + Hermans + LAR + dc). But knowing that we have a really small data-set (18 samples), we can’t use the 2-fold cross validation results as a decisive criteria. We decide to keep the predictive model dartdrop ~ dac + Hermans + LAR + dc for now. We can also observe the relative importance of each predictor in this model.
We did the same thing with the tear test mechanical properties (elmendorf TD and elmendorf MD). But the results will not be discussed in this post.
Regression results using the PCs as estimators
We then decide to generate some other prediction models using the PCs as estimators. The question is how many components do we need to use to get the best fit possible. We decided to generate several models while increasing the number of components.
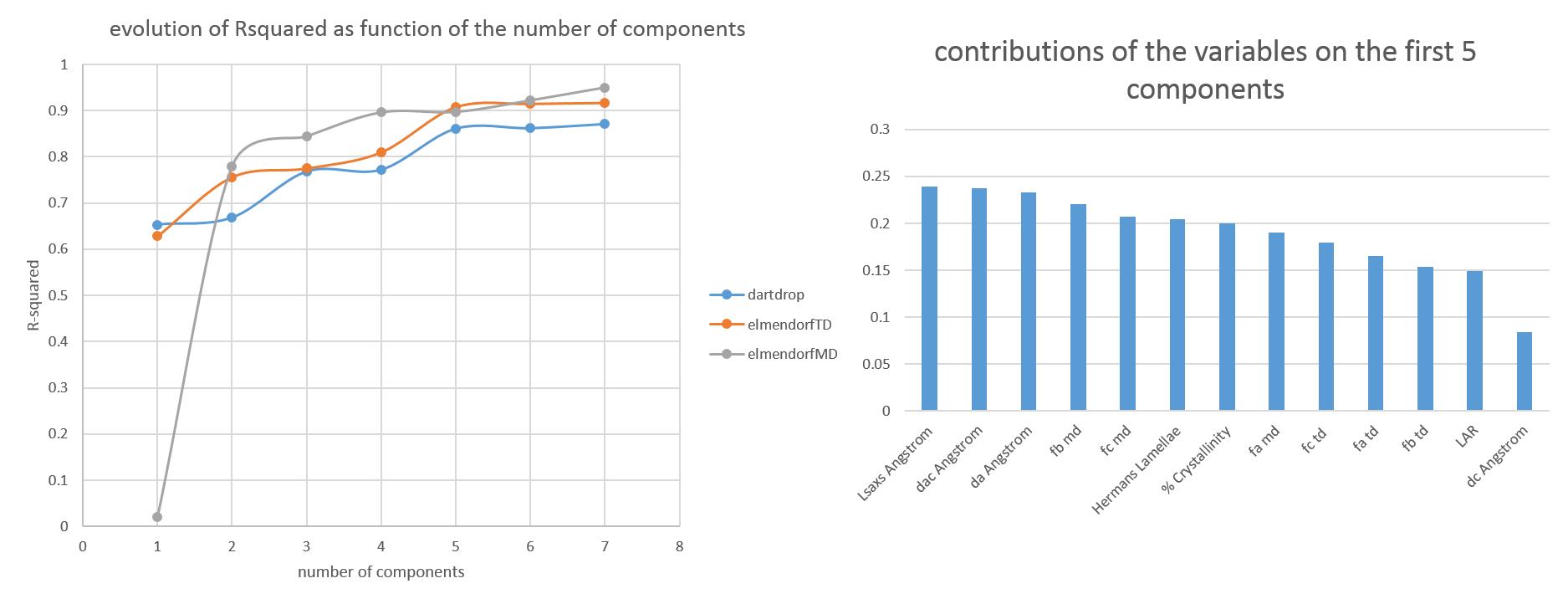
For all 3 mechanical properties, we can settle for a Rsquared close to 0.90. And in the 3 cases, we will need at least 5 principal components in the predictive model.