Cross-validation (CV)

Predicting the linkages in the Process-Structure-Property taxonomy requires the regression (continuous outputs) or classification (discrete outputs) from one class to another (i.e. Process to Structure).

Evaluating both regression and classification models is a challenging, but well established area. The most common method for estimating prediction error is cross-validation. The most common method for cross-validation is $K$ -fold cross validation, which splits the data into $K$ -folds, $K-1$ of which are used for training the model and the remaining for testing. This is repeated K times to yield a realistic view of the model performance.

$K$ -folds

How do we pick $K$ ? With $K = N$ , we have leave-one-out CV (LOO), the most commonly discussed method for this materials informatics course. In LOO the cv estimator is approximately unbiased, but the indvidual errors are likely to have high–possibly crippling–variance $^1$ . This is because each of the $N$ sets are very similar. On the other hand, 5-fold CV is more complicated as it offers a balance between lower prediction error variance and higher prediction error bias. Often 5- or 10-fold CV biases the prediction error estimates upwards, so that they appear larger than they would be when trained on the full data. Both 5- and 10-fold are a good balance between the LOO and 1-Fold extremes $^2$ . See work by Hastie et al. for further details.

Scikit-Learn makes CV Easy

from sklearn import cross_validation
	kfold = cross_validation.KFold(4, n_folds=2)
	cv_scores = cross_validation.cross_val_score(model, X, y, cv=kfold, n_jobs=1)
	#cv - the cross validation model you want to use
	#n_jobs - the number of processes to run in parallel (if model training is expensive)

Parameter Optimization

Many models have parameters, which dictate how the model performs during runtime. For example, in polynomial interpolation both degree and whether to fit an intercept are parameters. How can we select these to get the best performance in the face of overfitting?

Keep in mind that overfitting is a serious issue and can often be remedied with CV. We have implemented a pipeline that performs both CV and model parameter optimization using Scikit-Learn, pyMKS and NumPy.

Grid Optimization

We can explore the space of possible parameters by performing cross validation on each combination. Using the polynomial interpolation example above, consider the possible parameterizations: 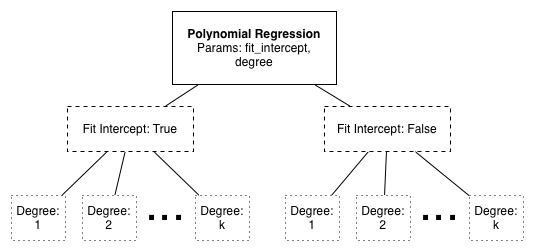gridcv Each leaf of this tree requires an entire $K$ -fold or LOO CV run.

Example Result

If you are using pyMKS to perform homogenization then you can actually use grid optimization on more than just the estimator parameters. The pyMKS homogenization model operates like a scikit learn model, so you can easily use it with grid optimization. You can use it on the whole homogenization pipeline (i.e. number of pca components, which correlations, etc.)! 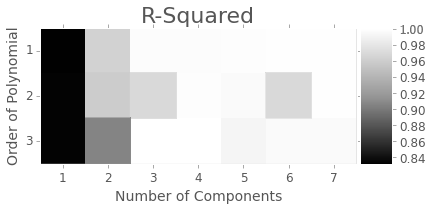gridcv Here’s an example result from when our pipeline was slightly abusing the process-structure pipeline code from pyMKS. It no longer does, so this plot is out of date, but proves that the optimization can be used well for homogenization. Thanks to David there’s even support to generate the plot above in just a line of code.

References

$^1$ Trevor Hastie, Robert Tibshirani, and Jerome Friedman. Springer Series in Statistics Springer New York Inc., New York, NY, USA, (2001)

$^2$ Leo Breiman and Philip Spector. Submodel Selection and Evaluation in Regression. International Statistical Review / Revue Internationale de Statistique, Vol. 60, No. 3. (Dec., 1992), pp. 291-319.