Cross-validation & Optimization

This post heavily utilizes cross-validation and parameter optimization. We have implemented a pipeline that performs both of these using Scikit-Learn, pyMKS and NumPy.

Our cross-validation module allows for different types of cross-validators.

Linear Models

We are working on our analysis of the different linear models and present the results below.

Linear Regression

Model form: $y_i = \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n + \epsilon$

More concisely: $y = X\beta + \epsilon$

This is a the ordinary least squares approach discussed in class.

Polynomial Fits

We used polynomial interpolation to model different potential representations for our data. We performed this by creating a new set of features consisting of the polynomial combinations of our features. We then performed OLS (ordinary least squares) linear regression on the new feature space to find the best fit in the new space. We tested only modest degrees as high degree polynomials are likely to heavily over-fit the our data.

Ridge Regression

Ridge model can be a better suited to make predictions. This model also has less variance than OLS. In OLS, we are looking for $\beta$ parameter, which we find by minimizing least squares of $(Y - X \beta)^2$ . However, in ridge model, a parameter $\alpha$ is used to bias $\beta$ to now minimize $||Y - X \beta||^2 +||\alpha \beta||^2$ . By introducing the $\alpha$ term, the values of parameter $\beta$ are now dependent on value of $\alpha$ . If $\alpha$ is increased, $\beta$ is forced to decrease. This is forcing large parameters to become smaller and might make the model avoid overfitting.

A closed form solution for parameters is the following: $\beta = (X^T X + \alpha I )^-1 X^T y$ if alpha is zero, then the model becomes an OLS.

Lasso Regression

This type of model is similar to Ridge in that there is a tuning parameter $\alpha$ . However, now the goal is to minimize $||Y - X \beta||^2 +||\alpha \beta||$ . The primary difference is that some of the $\beta$ parameters in Lasso model can become zero if they are not relevant in the model, whereas in Ridge all the parameters are kept non-zero.

Performance

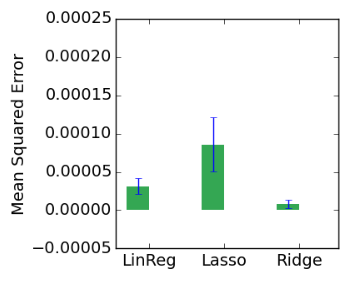mse Comparison of different linear models for preliminary results for linkage between PC space and solidification velocity (5-fold CV). Results show that Linear regression and Ridge models are better performers than Lasso.