Correlations in our data
We have about 20 simulations of a 3-phase solid. We have now reached a point in our investigation where we need to train on the transient data. Until now we have been naively using all 6 correlations in our PCA. Given that only (2 in our case) of these are dependent, we have decided to use only a subset of the original six; however, just because the remaining auto-and cross correlations are dependent does not mean that PCA and then regression will work equally well with any of the 15 combinations. This seemed like a good way to significantly reduce our computational costs, so we investigated the cost-benefits of using reduced correlations.
Testing Correlations as Inputs
As we only have 6 choose 2 possible pairs of correlations to use as inputs, we decided to simply brute-force our way to a solution.
We have tested each of the 15 possible Combinations of Al-Al, Ag-Ag, Cu-Cu, Al-Ag, Al-Cu, and Ag-Cu to see which performs best in our pipeline.
For each pair: we flatten the fields into a vector and perform PCA on it and then use our model optimization pipeline to find the optimal linear regression when tested with CV.
We report the values for each pair in the following matrix (self-pairs were ignored):
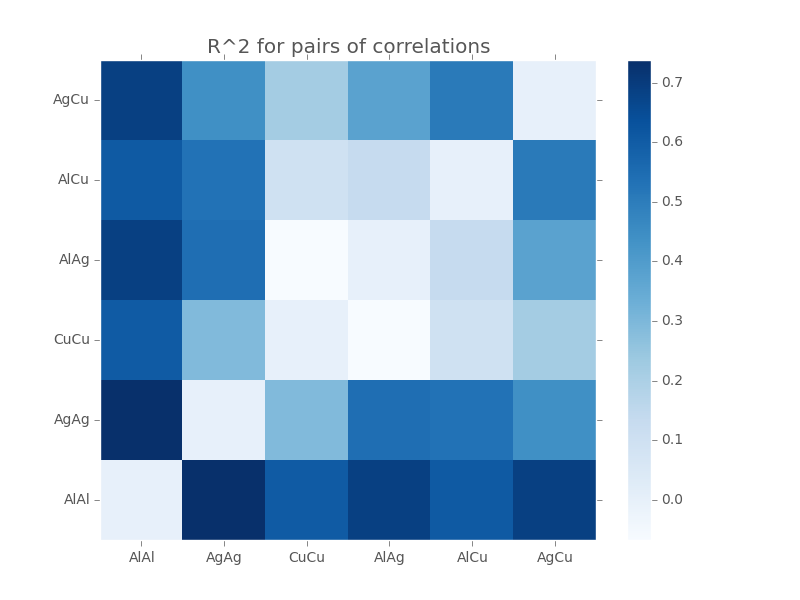
Why Al-Al and Ag-Ag
The pair, which performed the best, was surprisingly Al-Al and Ag-Ag (with Al-Al and Ag-Cu as the next runner up). It makes sense that we would want the Al-Al auto-correlation, because Al is the most prevalent state in our system and forms important channels between the striated Ag and Cu in the final results. Our hypothesis was that Al-Ag would be the logical secondary cross-correlation as it would provide critical detail in the interaction between the ‘rivers’ of Al and the striated Ag-Cu ‘islands’. Perhaps Al-Al covered enough about the structure of aluminum such that Al-Ag was less useful and therefore Ag-Ag or Ag-Cu provided the most missing information.
Reduced Correlations vs. Full Correlations
We then compared the results of the same optimization pipeline on the full set of 6 correlations against our abbreviated model.
The results really surprised us:
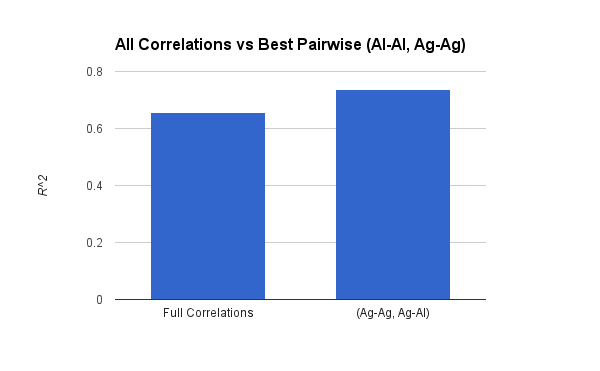We actually get slightly better results with the smaller model.
This may be because the extra information included in the remaining correlations serves only to introduce noise into the PCA and into the eventual linear solution.
We are looking deeper into why this is so.
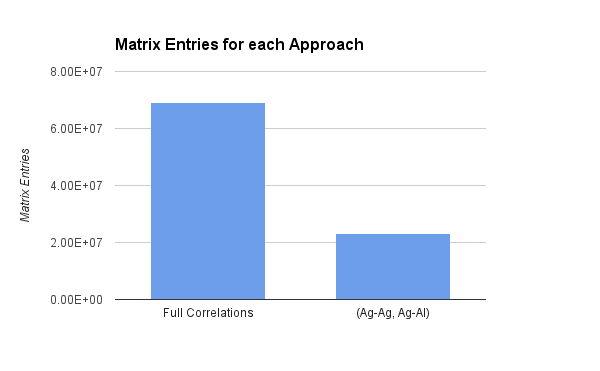
Savings!
This is a really good result for us as it not only saves a factor of 3 in the size of the PCA matrix (which we call very, very often when running our model optimization code), but also improves on our regression.
