Initial Superposition Results
During the initial verification procedure for MKS, only one tensor component was imposed with the other components were allowed to deform freely and the verification simulations were conducted under the same conditions. The strain are then dependent upon the Poisson ratio as the two free sides will contract when the third side is placed in uniaxial tension (lengthening). The second attempt utilized calibration coefficients from the single coefficient simulations. These resultant strains are applied to the predictive process previously explained to predict the full local response.
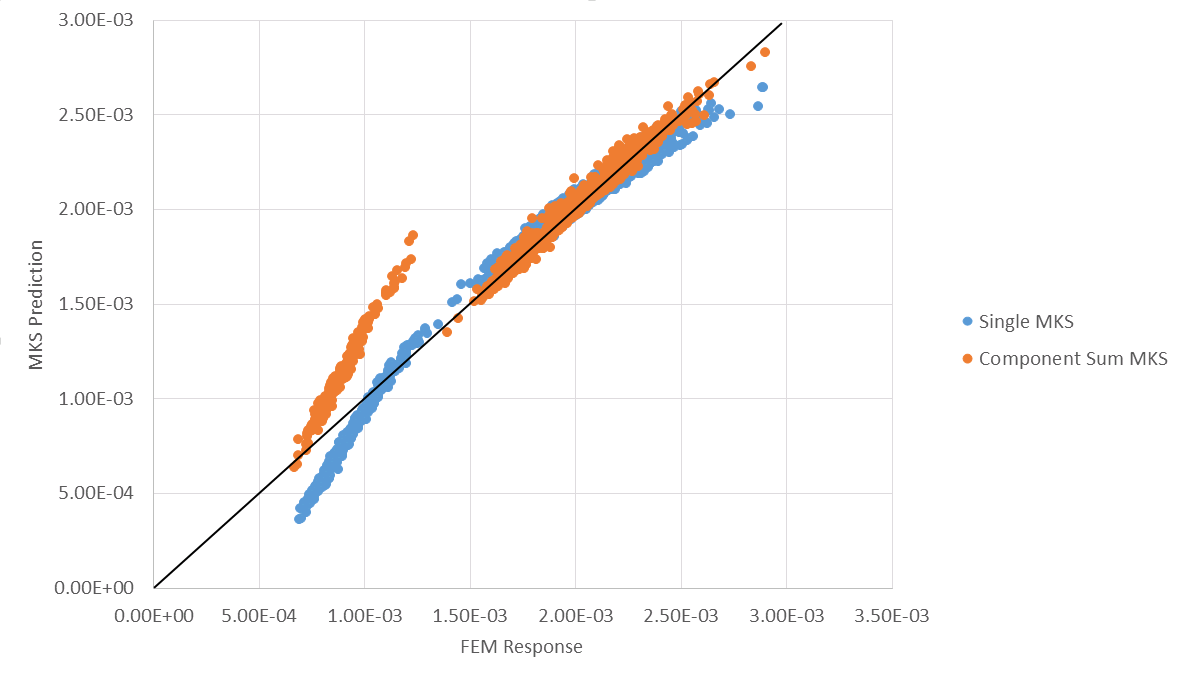
Based on some interesting effects observed in the error analysis, a comparison of the FEM simulations and the MKS simulations. Ideally the results would lie on a line with a slope of 1. The concerning part of this prediction is the dramatic shift of the prediction for the lower strain elements.
Attempt to Reconcile Prediction Errors
Given that the shift occurred in the lower strain elements, the assumption was that the particle elements were the ones being poorly predicted. Segmenting the plot confirmed this suspicion.
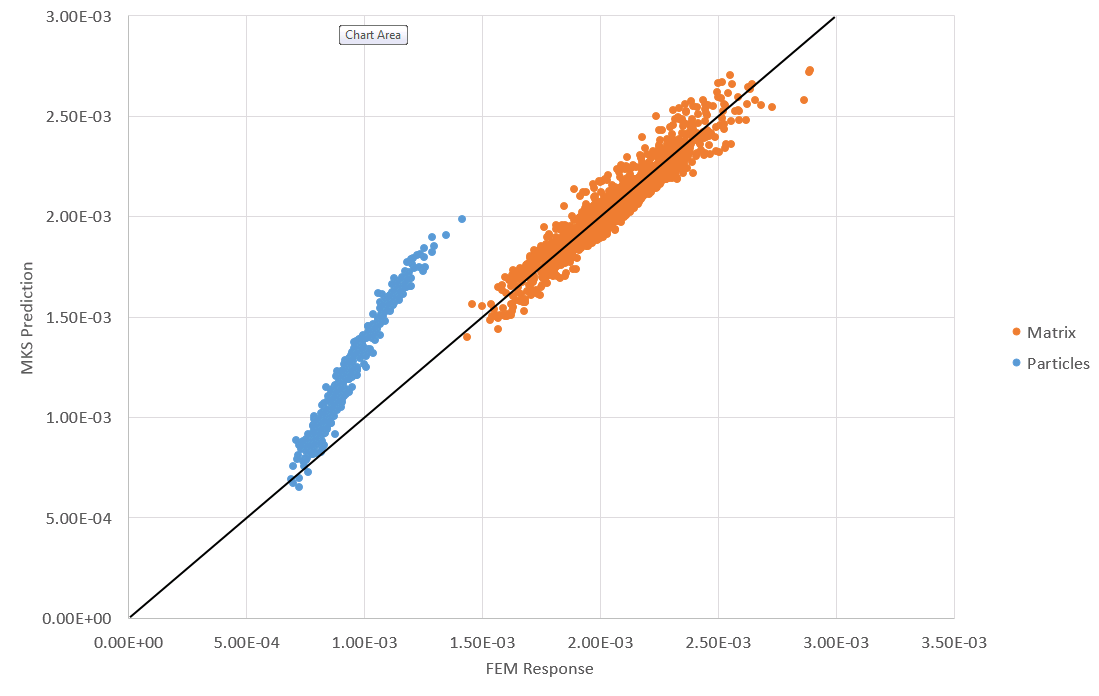
Once this was determined, additional assumptions were challenged in the MKS process. The periodic boundary conditions were verified by checking the displacements across the various faces. Additionally, the delta microstructures were verified and the Do note that the prediction is better in the top image as compared to the bottom using MKS because the entire strain tensor was predicted as a response to each imposed load and superposed in the top, compared to the bottom prediction which only scales the single tensor value corresponding to the imposed tensor value. The level of plasticity was computed to ensure that the assumption of elasticity is appropriate. The maximum values were less than 1% of the total strain in the respective element so this assumption appears to be valid. Finally, the same microstructure was tested with a loading condition that matches the loading condition for the single imposed strain component used for training (similar to how the single MKS prediction above used coefficients trained from the exact same macroscopic loading). This yielded a curve lacking the drastic jump visible in the first image for the superposition prediction. This verifies the prediction error is occurring due to the coefficients trained not being applicable for superposition.
Verification of Contrast Issues
After the previously discussed efforts to reconcile the errors in predicting the response of the hard particle phase, another final troubleshooting attempt was suggested in talking with Yuksel. As previously discussed, increased contrast between the phases can lead to increased error in predictions using the MKS method. Even though the ratio of the Young’s Modulus is only ~ 2.5, an additional source of contrast may have arisen due to the difference in the Poisson Ratio between the two phases. The difference between the particle ratio of 0.3 and matrix ratio of 0.36 could lead to complex interactions between the strain states that MKS is having trouble capturing. To eliminate this effect as a possibility, recalibration and testing will be performed with the Poisson Ratio of the particle phase increased to match that of the matrix.