Damage Prediction Methodology - Al7075-T6 Particle Distribution Impact on Multiaxial Lives

Assumptions

We have already addressed the most important limitation of the current single term MKS method and that is the prediction assumes linear elasticity. Since we will predict local damage based on the plastic strain tensor, the plastic strain must be a relatively small portion of the total strain. We verified this previously during the debugging of the MKS to be on the order of 1% of the total strain for the loading conditions imposed. Finally, to make predictions of plasticity relatively cheap we impose a further constraint of proportional loading. For the imposed strain tensor, all components must remain at the same ratios from 0 to the final applied load. This allows us to directly apply a hardening law based on the von Mises yield criterion.

Hardening Function

For a von Mises associated flow rule, we know that the incremental plastic strain is collinear with the incremental deviatoric stress tensor. For proportional loading this can be simplified to a function of the form $\bar{\varepsilon^{p}} = f(\bar{\sigma})$ Since we are doing a monotonic imposed strain, isotropic and kinematic hardening are both equivalent for the final stress state so we will assume isotropic for simplicity.

This function is stored in the form of tabulated data with a cubic interpolation function. The points selected from the FEM solution are highlighted in the following image.

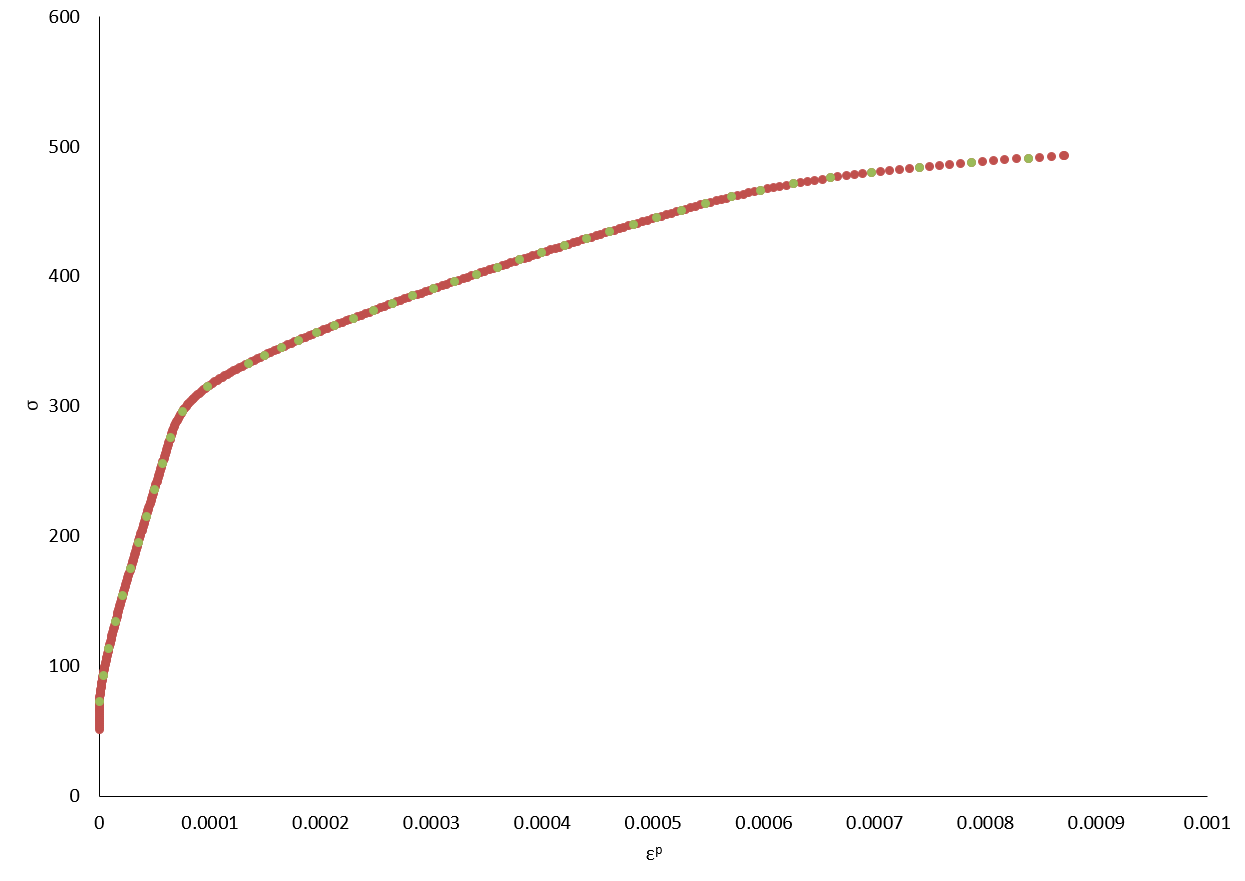
Damage Prediction

The overall stress tensor is predicted from a linear elastic stiffness with the predicted strain tensor

$\sigma = C\varepsilon$

The deviatoric tensor is then the subtraction of the hydrostatic stress from the stress tensor

$S = \sigma - I\frac{tr(\sigma)}{3}$

von Mises stress is represented by

$\bar{\sigma} = \sqrt{\frac{3}{2}S_{ij}S_{ij}}$

from there we acquire the equivalent plastic strain via our FEM data and apply this proportionally to the $S$ tensor to yield the final $\varepsilon^{p}$ tensor which is used in the damage prediction

$FIP_{FS} = \frac{\delta\gamma^p}{2} \left( 1 + k\frac{\sigma}{\sigma_y} \right)$

and $\frac{\Delta\gamma^p}{2}$ is taken to be the difference in the maximum and minimum principal plastic strains.