Truncation of Spatial Statistics
We realized that we can reduce our microstrucure images to a certain ‘truncated’ size while still retaining all the necessary structure information to represent the spatial statistics. This is one of the recent optimizations will that enable us to save computing time and memory in our project pipeline.
Our current microstructures are 800x800 pixels, and therefore out spatial correlations are also 800x800, per correlation. Truncation will be performed on the microstructures, for which spatial correlations will be calculated. An example of square truncation is shown below.
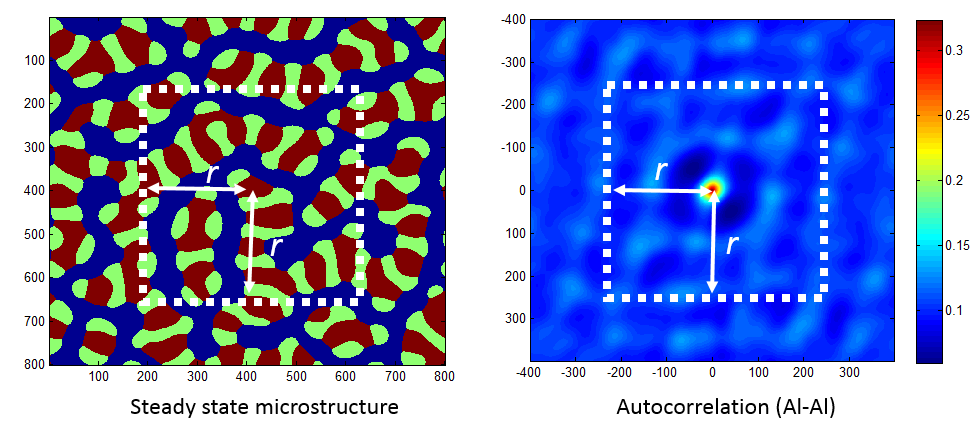
Vector Size Trucation
Above a certain vector size, the two point statistics oscillate around a value for which the probability between two local states becomes independent of each other. In other words, the probability of finding state h and h’ are not dependent on ecah other, . So for autocorrelation, the threshold at wich the statistics become independent is and for cross-correlation, . We also used a tolerance of 5%, meaning that values above 5% of the threshold were acceptable as independent probability.
Looking at the probabilities in the horizontal direction, as shown in the two image below, we see that the probability varies with vector size. In the second image, the probability is compared with the threshold value for one microstructure.

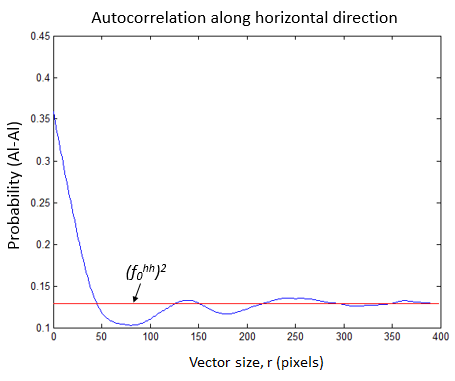
Looking at all the rest of the datasets, we took the average of all the 2-point statistics (Al-Al, and Ag-Ag) for steady-state microstructures in our 21 datasets and repeated the recorded how many points are above our threshold values. Threshold values vary based on the dataset. Below is a representation of the how many points are above the threshold in horizontal and vertical directions based on the vector size.
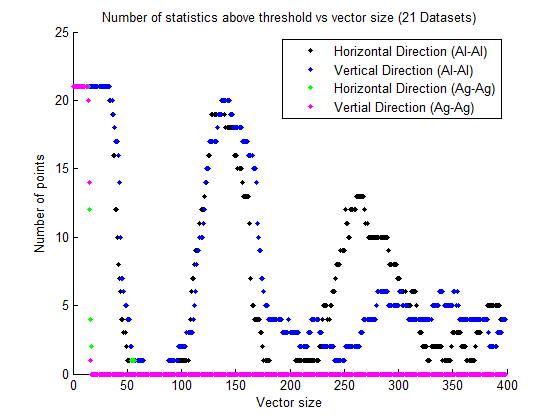
Based on the above plot we can see that truncating at vector size of 200 would be reasonable. For 21 datasets, the number of probabilities that are still dependent (conditional) in the truncated area is low, less that 4%.