Initial notes
We would like to explore microstructure recovery methods for our scatter plots. The first nuance to note is that our intensity plots represents an autocorrelation of a non-eigen microstructure in fourier space. We find the autocorrelation of our microstructure in real space (our statistics), by taking the inverse fourier transform of the raw intensity image and normalizing.
These statistics found from the intensity image to a characteristic equation defined below. We will apply this characteristic equation to simulated microstructures in order to have a frame of reference for this type of statistics.
Application of the characteristic equation
A good amount of time has been spent trying to acquire 2-pt statistics through various means of scaling and applied corrections. In the equation given here we see that taking the inverse fourier transform of the intensity data and normalizing results in data that can be directly correlated to volume fraction and 2-pt statistics. This characteristic equation serves as our statistics of the microstructure. We want to leverage our understanding of the characteristic equation given by $\gamma(r)$ to attempt microstructure recovery. The discretized version of this equation is shown below [1].
Data in data out
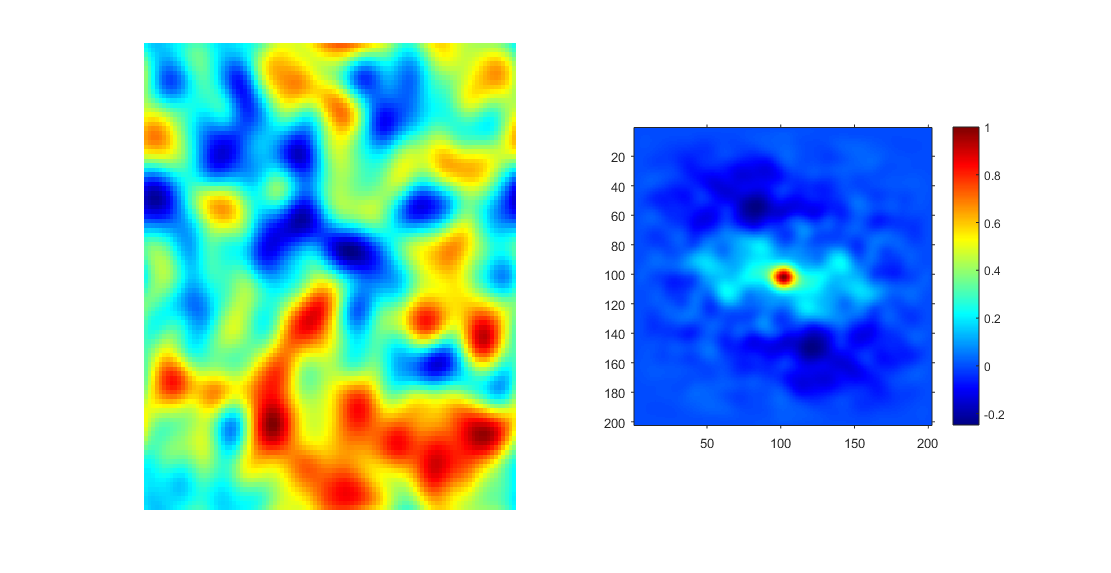
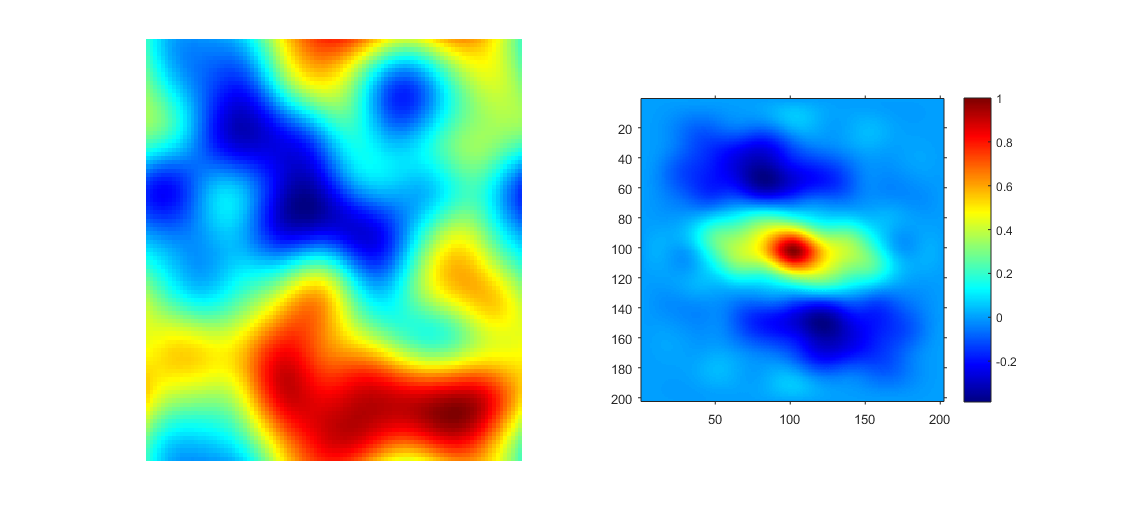
The domain of the normalized autocorrelation given by $\gamma(r)$ is -1 to 1 while $\gamma(0)=1$ and $\gamma(inf)=0$. The function is an autocorrelation of the microstructure allowing us to apply DFTs to make the calculation fast. The simulated microstructures allow us to become more comfortable with the statistics we find from the intensity images. Modifying some tools in PYMKS allows us to generate non eigen microstructures and vary rudimentary parameters pertaining to shape and size. The simulated microstructures are on the left and the output of the charateristic equation from these microstructures are shown on the right. A future post will compare these results using the characteristic equation with results from our actual images.
Small sized microstructures
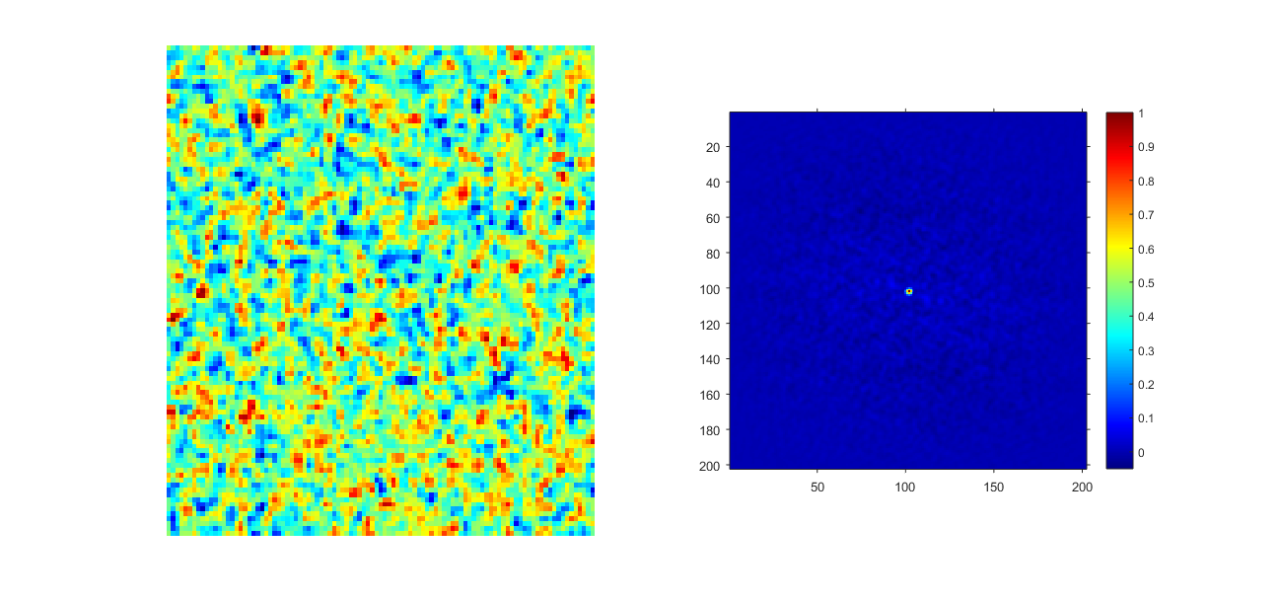
Medium sized microstructures
Large sized microstructures
Sources
[1] L.A. Feigin, D.I. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, pg 41 [2] R. J. Roe, Methods of X-Ray and Neutron Scattering in Polymer Science, 174-176, Oxford University Press 2000.